|
M.Ö
20 yy
|
Babilliler;
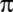 =
31/8 değerini kullanıyorlar. =
31/8 değerini kullanıyorlar.
|
|
M.Ö
20 yy
|
Mısırlılar;
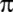 =
(16/9)*(16/9)= 3,1605 değerini kullanıyorlar. =
(16/9)*(16/9)= 3,1605 değerini kullanıyorlar.
|
|
M.Ö
12 yy
|
Çinliler;
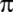 =
3 değerini kullanıyorlar. =
3 değerini kullanıyorlar.
|
|
M.Ö
550
|
Kutsal Kitapta I.Krallar;
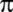 =
3 değerini kullanıyorlar. =
3 değerini kullanıyorlar.
|
|
M.Ö
434
|
Anaksagoras; daireyi kare yapmaya çalışıyor.
|
|
M.Ö
3 yy
|
Arşimed; 310/71 <
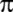 <
31/7 olduğunu buluyor. Bundan başka <
31/7 olduğunu buluyor. Bundan başka
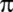 =
211875/67441 kesrini de buluyor. =
211875/67441 kesrini de buluyor.
|
|
2.
yy
|
Batlamyos;
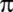 =
377/120 = 3,14166... değerini kullanıyor. =
377/120 = 3,14166... değerini kullanıyor.
|
|
3.
yy
|
Çung Hing;
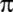 =
3,16; Vang Fav; =
3,16; Vang Fav;
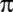 =3,155;
Liu Hui; =3,155;
Liu Hui;
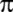 =
471/150 = 3,14 değerlerini kullanıyorlar. =
471/150 = 3,14 değerlerini kullanıyorlar.
|
|
5.
yy
|
Zu Çung Çi; 3,1415926 <
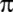 <3,1415927
olduğunu buluyor. <3,1415927
olduğunu buluyor.
|
|
6.
yy
|
Hintli Aryabhatta;
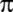 =
62832/2000 = 3,1416 değerini, Brahmagupta; =
62832/2000 = 3,1416 değerini, Brahmagupta;
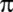 =
kök 10 değerini kullanıyorlar. =
kök 10 değerini kullanıyorlar.
|
|
1220
|
Fibonacci;
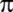 =
3,141818 değerini kullanıyor. =
3,141818 değerini kullanıyor.
|
|
1436
|
Semerkantlı El Kaşi;
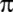 'yi
14 basamağına kadar hesaplıyor. 'yi
14 basamağına kadar hesaplıyor.
|
|
1573
|
Valentinus Otho;
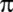 =
355/113 = 3,1415929 olduğunu buluyor. =
355/113 = 3,1415929 olduğunu buluyor.
|
|
1593
|
Hollandalı Adriaen van Rooman;
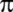 'yi
15 basamağına kadar hesaplıyor. 'yi
15 basamağına kadar hesaplıyor.
|
|
1596
|
Hollandalı Ludolph Van Ceulen;
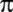 'yi
35 basamağa kadar hesaplıyor.(Bu nedenle Almanya'da 'yi
35 basamağa kadar hesaplıyor.(Bu nedenle Almanya'da
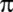 ;
Ludolph Sayısı olarak bilinir.) ;
Ludolph Sayısı olarak bilinir.)
|
|
1705
|
Abraham Sharp;
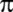 'yi
72 basamağa kadar hesaplıyor. 'yi
72 basamağa kadar hesaplıyor.
|
|
1706
|
John Machin;
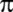 'yi
100 basamağa kadar hesaplıyor. 'yi
100 basamağa kadar hesaplıyor.
|
|
1719
|
Fransız De Lagny;
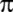 'yi
127 basamağa kadar hesaplıyor. 'yi
127 basamağa kadar hesaplıyor.
|
|
1737
|
Leonhard Euler; 'in benimsemesiyle
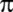 adı
evrensellik kazanıyor. adı
evrensellik kazanıyor.
|
|
1761
|
İsviçreli Johann Heinrich Lambert;
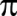 'nin
irrasyonelliğini kanıtlıyor. 'nin
irrasyonelliğini kanıtlıyor.
|
|
1775
|
Euler;
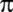 'nin
olabileceğine işaret ediyor. 'nin
olabileceğine işaret ediyor.
|
|
1794
|
Fransız Adrien-Marie Legendre;
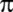 'nin
ve 'nin
ve
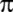 * *
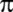 'nin
irrasyonelliğini kanıtlıyor. Aynı zamanda 'nin
irrasyonelliğini kanıtlıyor. Aynı zamanda
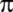 'nin
aşkın olabileceğini belirtiyor. 'nin
aşkın olabileceğini belirtiyor.
|
|
1794
|
Vega;
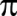 'yi
140 basamağa kadar hesaplıyor. 'yi
140 basamağa kadar hesaplıyor.
|
|
1844
|
Avusturyalı Schulz von Stranssnigtzky;
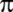 'yi
200 basamağa kadar hesaplıyor. 'yi
200 basamağa kadar hesaplıyor.
|
|
1855
|
Richter;
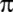 'yi
500 basamağa kadar hesaplıyor. 'yi
500 basamağa kadar hesaplıyor.
|
|
1874
|
İngiliz W. Shanks;
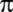 'yi
707 basamağa kadar hesaplıyor. 'yi
707 basamağa kadar hesaplıyor.
|
|
1882
|
Alman Ferdinand Lindemann;
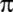 'nin
aşkın bir sayı olduğunu kanıtlıyor. 'nin
aşkın bir sayı olduğunu kanıtlıyor.
|
|
1947
|
İlk bilgisayar ENIAC;
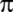 'yi
2035 basamağa kadar hesaplıyor. 'yi
2035 basamağa kadar hesaplıyor.
|
SAYISININ
PİSAGOR BAĞINTISINDAN YARARLANILARAK BULUNMASI
1-
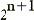 KENAR
SAYISI OLMAK ÜZERE, BİR DAİRE İÇİNDE KİRİŞ OLUŞTURAN BİR KENAR UZUNLUĞUNUN
4, 8, 16, 32 GEN'LER OLUŞTURACAK ŞEKİLDE ÇOĞALTILIP ELDE EDİLEN
UZUNLUKLARIN
KENAR
SAYISI OLMAK ÜZERE, BİR DAİRE İÇİNDE KİRİŞ OLUŞTURAN BİR KENAR UZUNLUĞUNUN
4, 8, 16, 32 GEN'LER OLUŞTURACAK ŞEKİLDE ÇOĞALTILIP ELDE EDİLEN
UZUNLUKLARIN
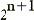 İLE
ÇARPIMININ, ÇAPA BÖLÜNEREK
İLE
ÇARPIMININ, ÇAPA BÖLÜNEREK
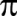 'NİN BULUNMASI. BİRİM 2r=1
'NİN BULUNMASI. BİRİM 2r=1
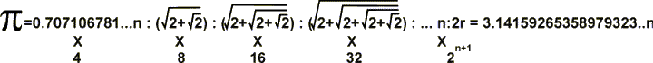
2-
3 x
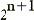 KENAR
SAYISI OLMAK ÜZERE BİR DAİRE İÇİNE ÇİZİLEN EŞKENAR ÜÇGENİN DAİRE
İÇİNDE KİRİŞ OLUŞTURAN BİR KENAR UZUNLUĞUNUN 3, 6, 12, 24 GEN'LER OLUŞTURACAK
ŞEKİLDE ÇOĞALTILIP ELDE EDİLEN UZUNLUKLARIN 3 x
KENAR
SAYISI OLMAK ÜZERE BİR DAİRE İÇİNE ÇİZİLEN EŞKENAR ÜÇGENİN DAİRE
İÇİNDE KİRİŞ OLUŞTURAN BİR KENAR UZUNLUĞUNUN 3, 6, 12, 24 GEN'LER OLUŞTURACAK
ŞEKİLDE ÇOĞALTILIP ELDE EDİLEN UZUNLUKLARIN 3 x
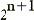 İLE
ÇARPIMININ, ÇAPA BÖLÜNEREK
İLE
ÇARPIMININ, ÇAPA BÖLÜNEREK
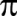 SAYISININ BULUNMASI. BİRİM
2r=1
SAYISININ BULUNMASI. BİRİM
2r=1
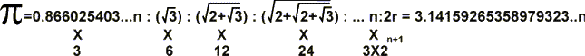
3-
BİRİM DAİRE İÇİNE ÇİZİLEN KARE'NİN ALANINDAN YARARLANILARAK , BİRİM
DAİRENİN ALANININ HESAPLANARAK r 2 'YE BÖLÜNEREK
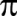 SAYISININ BULUNMASI. BİRİM 2r
= 1
SAYISININ BULUNMASI. BİRİM 2r
= 1
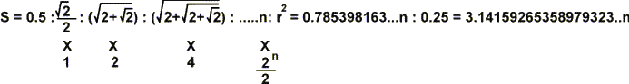
4-
BİRİM DAİRE İÇİNE ÇİZİLEN EŞKENAR ÜÇGENİN ALANINDAN YARARLANILARAK,
BİRİM DAİRENİN ALANININ HESAPLANARAK r 2 'YE BÖLÜNEREK
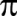 SAYISININ BULUNMASI. BİRİM 2r
= 1
SAYISININ BULUNMASI. BİRİM 2r
= 1
5-
TÜM BU İŞLEMLERDEN SONRA
 SAYISININ BULUNABİLMESİ İÇİN
GENEL İFADE YAZMAK İSTERSEK ,
SAYISININ BULUNABİLMESİ İÇİN
GENEL İFADE YAZMAK İSTERSEK ,
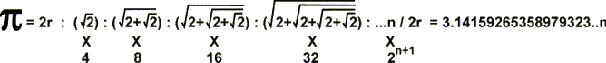
EŞİTLİĞİ
ORTAYA ÇIKAR.
NOT:
YUKARIDAKİ FORMÜLLERDE
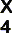 vs. İLE
GÖSTERİLEN SAYILAR İŞLEM BELİRLİ BİR NOKTADA KESİLMEK İSTENDİĞİNDE
İFADENİN SON OLARAK ÇARPILACAĞI KATSAYILARDIR. İŞLEM KESİLDİĞİ
NOKTADAN ÖNCE FORMÜLÜN ALTINDA VERİLEN KATSAYILAR DİKKATE ALINMAMALIDIR.
vs. İLE
GÖSTERİLEN SAYILAR İŞLEM BELİRLİ BİR NOKTADA KESİLMEK İSTENDİĞİNDE
İFADENİN SON OLARAK ÇARPILACAĞI KATSAYILARDIR. İŞLEM KESİLDİĞİ
NOKTADAN ÖNCE FORMÜLÜN ALTINDA VERİLEN KATSAYILAR DİKKATE ALINMAMALIDIR.
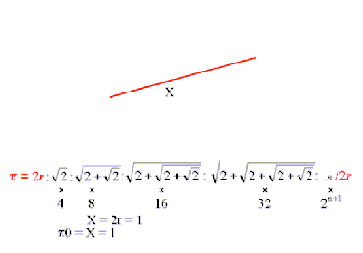
DEVAM ETTİĞİNİZ TAKTİRDE
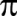 SAYISINA VARILIR.
SAYISINA VARILIR.