FİBONACCİ

Papatya

Zambak

Ayçiçeği

Ananas

FİBONACCİ KİMDİR?

Orta çağın en büyük matematikçilerinden biri olarak  kabul edilen Fibonacci İtalya'nın ünlü Pisa şehrinde doğmuştur. Çocukluğu babasının çalıştığı Cezayir'de geçmiştir. İlk matematik eğitimini Müslüman bilim adamlarından almış ve İslam aleminin kitaplarını incelemiş ve çalışmıştır. Avrupa'da Roma rakamları kullanılırken ve sıfır  kavramı ortaalrda yokken Leonarda Arap rakamlarını ve sıfırı öğrenmiştir.

1201 yılında "Liber Abacci" (cebir kitabı manasına gelir) adında bir matematik kitabı yazmıştır. Bu  kitapla Avrupa'ya Arap rakamlarını ve bugün kullandığımız sayı sistemini tanıtmıştır. Bu kitapta, ilkokulda öğrendiğimiz temel matematik  ( toplama, çarpma, çıkartma ve bölme ) kurallarını bir çok örnek vererek anlatmıştır.

İsterseniz 1200 lü yılllarda Avrupa'da kullanılmakta olan Roma Rakamlarına bir bakalım ve onlarla işlem yapmanın ne kadar zor olduğunu görelim

Roma Rakamları

I = 1 , V = 5,  X = 10,  L = 50, C = 100, D = 500, M = 1000

Bu rakamlarla 13 XIII ve ya IIIX şeklinde, 2003 MMIII şeklinde, 99 LXXXXVIIII şeklinde ve 1998 MDCCCCLXXXXVIII şeklinde yazılır.

CCXXIII + XXVIII = CCI

CLXXIIII -  XXVIII = CXXXXVI

Tahmin edebileceğiniz gibi Roma Rakamları ile aritmetik işlemleri yapmak hiçte kolay değildi.

FİBONACCİ SAYILARI

Gelelim Fibonacci'nin ünlü sorusuna..

"Bir çift yavru tavşan( bir erkek ve bir dişi) var. Bir ay sonra bu yavrular erginleşiyor.. Erginleşen her çift tavşan bir ay sonra bir çift yavru doğuruyorlar. Her yavru tavşan bir ay sonra erginleşiyorlar. Hiç bir tavşanın ölmediğini ve her dişi tvşanın bir erkek bir dişi yavru doğurduğunu varasayalım.   Bir yıl sonra kaç tane tavşan olur?"

1. İlk ayın sonunda ,  sadece bir çift vardır.
2. ikinci ayın sonunda  dişi bir çift yavru doğurur, ve elimizde 2 çift tavşan vardır.
3. Üçüncü ayın sonunda,  ilk dişimiz bir çift yavru doğurur, 3 çift tavşanımız olur
4. Dördüncü ayın sonunda , ilk dişimiz yeni bir çift yavru daha doğurur, iki ay önce doğan dişi de bir çift yavru doğurur ve 5 çift tavşanımız vardır.

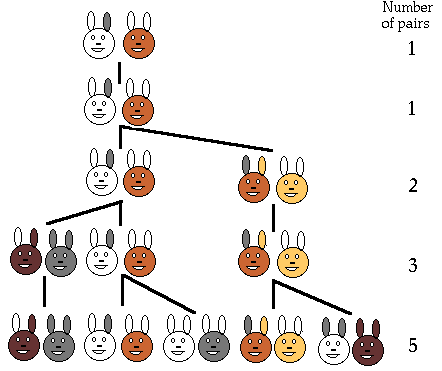
Bu şekilde devam ederek  şu diziyi elde ederiz: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,89, 144

Dizideli sayılar Ocak (ilk yavru çiftinin olduğu ay)  ile Aralık arasındaki ayların her birinde kıtır kıtır havuç yiyen tavşan çiftlerinin sayısını vermektedir.

Serinin nasıl oluştuğunu anlayabildiniz mi? Bu dizi çok basit şekilde oluşmaktadır. Bu dizideki her sayı (ilk ikisi dışında) kendinden evvel gelen iki sayının toplamına eşittir.

Peki, bu diziyi böylesine ilginç kılan nedir?   Bunu üç ayrı nedene bağlayabiliriz.

1.      İlk  olarak dizinin küçük üyelerinin doğada, beklenmedik yerlerde karşımıza çıkmasıdır.; bitkiler, böcekler, çiçekler vb. şeylerle ilgili olarak..

2.      İkinci neden,  oranların limit değeri olan 0,618033989 sayısının çok öenmli bir sayı olmasıdır. ALTIN ORAN diye adlandırılan bu sayı Leonardo da Vinci'nin resimlerinden eski Yunan tapınaklarına kadar bir çok sanat eserinde ve doğada karşımıza çıkan bir sayıdır.

3.      Üçüncüsü ise sayılar teorisinde beklenmedik biçimde farklı bir çok kullanımı olmasıdır.

FİBONACCİ SAYILARI VE ALTIN ORAN

Fibonacci serisindeki n. terimi Fn olarak ifade edelim. Fibonacci dizisi bu şekilde F1, F2, F3, ...., Fn,....

olarak yazılabilir. bu dizi sonsuza kadar devam eder.

eğer her Fibonacci sayısını bir sonraki komşusuyla bölerek bu oran yazılırsa,

F1/F2 = 2, F2/ F3 = 1/2 .. şeklinde devam edersek aşağıdaki diziyi elde ederiz.

bu sayılar bir 0,618034... sayısına doğru gidiyorlar. Altın oran 1,618... ve bu limit de onun ondalık kısmı

FİBONACCİ SAYILARI VE BİTKİLER

Eğer bir bitkiyi dikkatle incelerseniz farkedersiniz ki, yapraklar ,hiç bir yaprak altaki yaprağı kapmayacak şekilde dizilmiştir. Bu da demektir ki, her bir yaprak güneş ışığın eşit bir şekilde paylaşıyor ve yağmur damlaları bitkinin her bir yaprağına değebiliyor.

Bir bitkinin sapındaki yaprakların, bir ağacın dallarının üzerinde hemen her zaman Fibonacici sayıları bulursunuz. Eğer yapraklardan biri başlangıç noktası olarak alınırsa ve bundan başlayarak, aşağıya ya da yukarıya doğru, başlangıç noktasının tam üstünde veya altında bir yaprak buluncaya kadar yapraklar sayılırsa bulunan yaprak sayısı farklı bitkiler için değişik olacaktır ama her zaman bir Fibonacci sayısıdır.

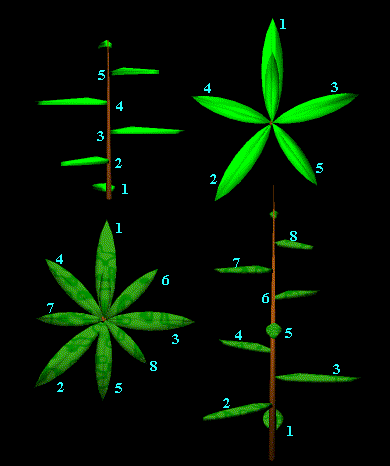
Mesela, yandaki resimde en baştaki dalı incelersek, başlangıç noktası olarak 1 numaralı yaprağı alırsak, kendisiyle aynı yönde bir başka yaprakla karşılaşabilmemiz için 3 defa saat yönünde bir dönüş yapmamız gerekir ve bu esnada 5 tane yaprak sayarız. Eğer bu dönüşü saat yönünün tersinde yaparsak 2 tane dönüş gerekecektir. Ve 2, 3, 5 ardışık fibonacci sayılarıdır.

Yandaki resimde yer alan dalı incelediğimizde ise 8 yaprak üstünden geçtiğimiz 5 tane saat yönünde dönüş yaparız. Saat yönünün ters istikametinde ise bu dönüş sayısı 3 olacaktır.

3, 5, 8 ise ardışık Fibonacci sayılarıdır.

Bunu en üsteki bitki için şöyle de yazabilirsiniz. 3/5 (saat yönündeki dönüş başına yaprak sayısı)

Doğada yer alan ağaçlar için bu sayılar şöyle yazılabilir.

Karaağaç, Ihlamur Ağacı, çimen : 1/2

Kayın Ağacı, fındık Ağacı, Böğürtlen :1/3

Meşe, elma ağacı, kiraz ağacı: 2/5

FİBONACCİ SAYILARI VE ÇİÇEKLER

Bir çok çiçeğin taç yaprak sayısı Fibonacci saysısıdır.

3 taç yapraklı bitkiler: zambak,  iris

5 taç yapraklı bitkiler: düğünçiçeği, yabani gül,  hezaren çiçeği

8 taç yapraklı bitkiler: delphinium

13 taç yapraklı bitkiler:  kanaryaotu, kadife çiçeği,   cineraria

21 taç yapraklı bitkiler: hindiba, yıldız çiçeği

34 taç yapraklı bitkiler:  bir çeşit muz bitkisi, pirekapan

55, 89 taç yapraklı bitkiler: bir tür papatya

FİBONACCİ SAYILARI VE BİTKİ TOHUMLARI

Fibonacci sayıları ayrıca çiçeklerin tohumlarında da görülebilir. Eğer bir papatyanın ve ya bir ayçiçeğinin çiçek kısmını büyütseniz muhtemelen yandaki resme benzer bir görüntü elde edersiniz.

Eğer şekildeki modelde, saat yönünde olan ve saaat yönünde olmayan sarmalları sayarsanız, 21 ve 34  sayılarını elde edersiniz ki bu sayılar ardışık iki fibonacci sayısııdır.

Fibonacci sayılarına sadece ayçiçeklerinde ve ya papatyalarda değil, bir kıvırcığın yapraklarında bir ananas ve ya  kozalakların kat kat kabuklarında, soğanın katmanları arasında da rastlayabilirsiniz.

KOZALAKLAR

Kozalaklar fibonacci sayılarını çok açık bir şekilde gösterirler.   Kırmızı ve yeşil spiralleri saydığınızda ne görüyorsunuz?

(Resimlerin üzerine tıklayarak onları büyütebilirsiniz.)